#16: Notes on Arithmetic in GPT-4
A few weeks ago, I had a list of dollar amounts that I needed to sum up. I thought: “GPT is good at converting formats,” and copy-pasted them into ChatGPT.
The result looked plausible. But I had a moment of doubt: why should GPT be good at addition? So I double-checked the sum myself. It turned out that GPT was wrong; the right number was $660.44. Ever-so-slightly off.
This struck me as a very strange result, for two contradictory reasons:
It’s not surprsising that GPT is wrong. There’s nothing really about a language model that implies learning to sequentially apply the strict rules of arithmetic. While it’s possible to argue that GPT can reason if you give it some memory and many iterations over which its language inference turns into (fuzzy) symbolic inference,1 that’s not happening in a single ChatGPT query.
But then why is the result so close? It’s only wrong by 0.3%! Clearly there’s some kind of fuzzy symbolic inference getting made here that approximates addition pretty well.
This piqued my interest. My hypothesis was that the GPT-4 training set was so vast that it simply included many strings of arithmetic, which could then be recited verbatim for correct results, or used as a base for some token-level inference. Especially if there’s memoization at play, then this would explain good arithmetic performance even without the LLM actually conducting symbolic reasoning.
However, that’s a fragile process. If the above was true, then GPT should become less accurate as the arithmetic expressions became longer. I was curious what the relationship would look like, so I took an evening to run some experiments.
Experiment: Plain Arithmetic
You can follow along by looking through the code and data in my open-source repo.
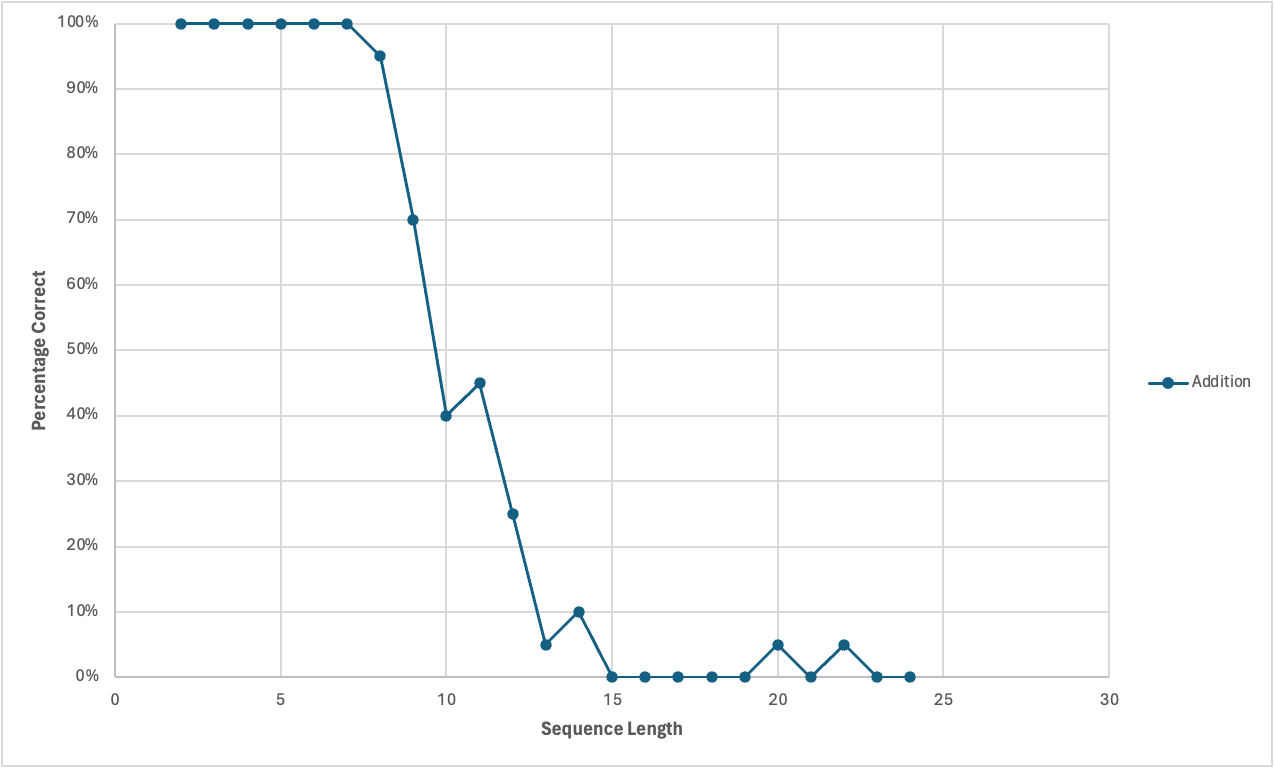
Addition
I created sequences of random integers between 1 and 100. I varied these sequences in length from 2 numbers all the way through 24 numbers, and joined them up with addition symbols.2 I used a prompt in which I asked GPT-4 to solve the arithmetic problem and to return strictly a number. I then evaluated the GPT-generated sum against the true sum, and measured what percentage matched exactly. For every sequence length, I took 20 samples, so the chart below represents 460 datapoints.
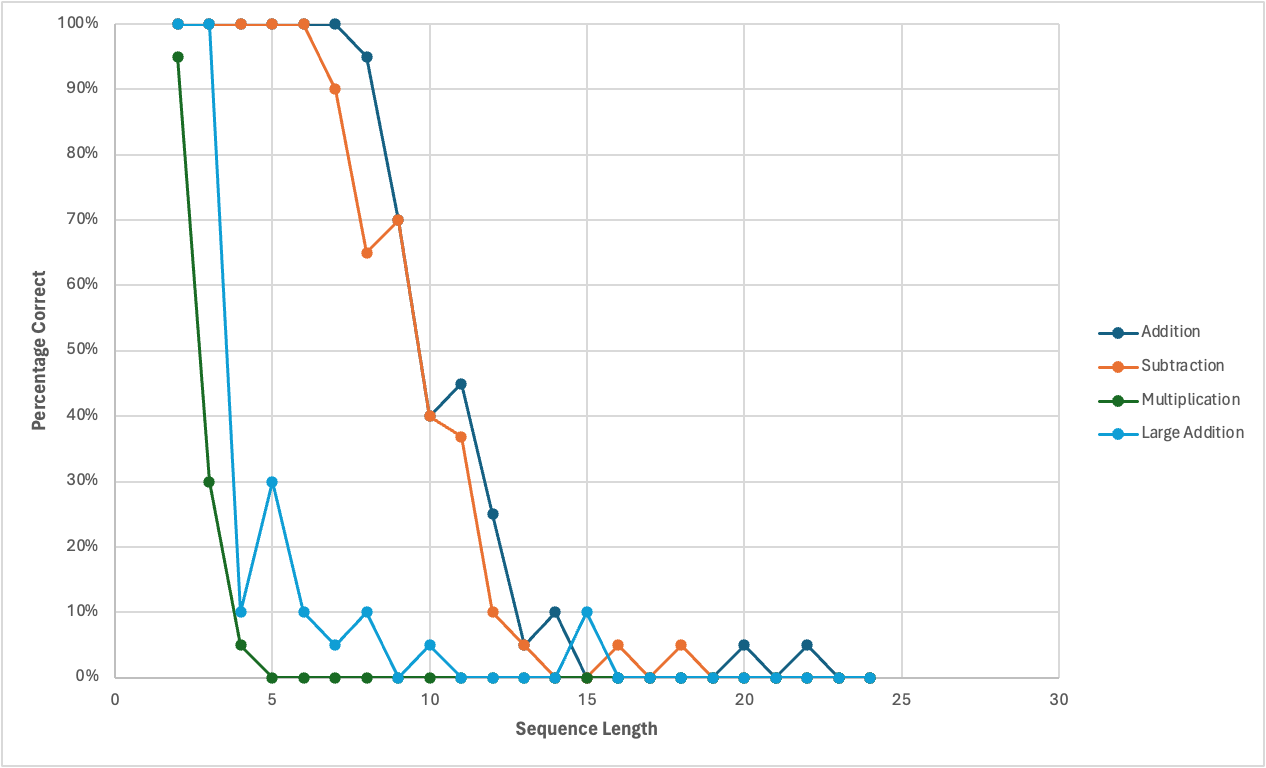
Subtraction
Same methodology. I expected addition to perform better than subtraction because addition is a much more common operation, but the results were quite similar.
Multiplication
Same methodology. Again, my guess was that accuracy would drop off faster than for addition or subtraction because there’s likely fewer such text samples online, and multiplication blows up the number of tokens: if you’re multiplying 20 numbers between 1 and 100, the result is going to be a long number — lots of digits — which increases the room for GPT to make mistakes.
As predicted, performance was much worse: GPT-4 had 95% accuracy for multiplying two numbers under 100, 30% accuracy for multiplying three, 5% accuracy for multiplying 4, and zero thereafter.
Large Addition
I wanted to further investigate the idea that GPT-4’s addition is good because there are many solved examples in its training data. I assumed that numbers under 100 are much better represented than large numbers, and was curious if performance would degrade if I used larger numbers instead. For this set, instead of generating random integers between 1 and 100, I generated random integers between 812,300 and 812,400. I figured these numbers were big enough that it’s unlikely for there to be lots of solved examples online.
The results bear this out: accuracy drops off much faster than for regular addition, but it still stands out as remarkable to me that it’s scoring 100% accuracy on 2- and 3-number sequences. (We’ll come to why this is important in a later section.)
Addition by Sum
We observed that changing the operator from addition to multiplication, for example, is accompanied by degradation in performance. But what if you just change the syntax? Does “sum of 2, 3, 4” perform differently from “2 + 3 + 4”? Again, my hunch was that “sum” would perform worse because it’s a less commonly used syntax.
It turns out that the sum syntax performs much better than regular addition. If you’re surprised, I was too!
The implication is that “+” and “sum” are not represented the same way internally by GPT-4.34 If the results were the same, or close, then there would’ve been a conclusion to draw about GPT internally transforming different syntaxes of equivalent inputs into the same format — but that is not so. This is noteworthy to me because syntax/format transformation5 is a task that GPT is usually strong at. But I suppose that transformation for output is not the same as transformation for internal processing.
How Far Off?
We know that GPT becomes likelier to make an arithmetic error the longer the expression is. But how severe are these errors? The example from the very start, which motivated this entire investigation, was off by only 0.3%.
I took the Large Addition dataset (adding numbers between 812,300 and 812,400), and took a look at how far off the GPT-generated result was on average:
These are pretty close! But looking at the average % deltas obscures some of the detail. Below are the actual results for the sequence of length 24:
What’s interesting is that these results are very consistent: the delta is either around 0.20% or around -16.67%. This suggests that there are two different ways that these prompts get handled by GPT. The 0.2% delta way is clearly both hallucinating but also approximating closely the results of actual6 addition.
Symbolic Reasoning for Addition?
Earlier I mentioned that even in the Large Addition case, it maintained 100% accuracy for 2- and 3-integer sums. But maybe those numbers were too small? I tested with even larger numbers.
Most of these are right. (70% correct.) The ones that are wrong are wrong in interesting ways — row 2 is just off by four, rows 7, 9, 10, 11 all have the thousands digit too low by one. Row 17 just has one extraneous digit. This feels similar to the “How Far Off” section just earlier; where maybe there are several internal paths by which GPT may handle these computations — some of them work, and others don’t.
Can I force GPT into the “right” path? My first hunch was that the “wrong” paths were probably downstream of some of the internal randomness of the LLM. There’s a way to control this: the temperature parameter.
So I set the temperature to zero, and ran a 400-sample experiment for the same number range. The results improved from 70% to 93.5%. The errors were the same types as above, mostly one digit too low in the thousands place.
Could I improve it further? I wrote a “stronger” prompt admonishing the LLM to use its best technique and fiddle with the results, and again ran a 400-sample experiment. The results improved further to 97.5%.7
It appears that the LLMs contain some pathways for achieving correct addition, and we are able to (approximately) unlock them by querying the LLM in particular ways. If such correct addition is purely generated by the LLM (and not any additional logic like built-in arithmetic tables), then this suggests that the LLM’s language inference somehow is conducting actual symbolic reasoning at small scale. Not reliably all the time, but the fact that it’s doing it at all is remarkable, in and of itself.
This is a sign of what’s to come in the future. The big limitation of LLMs at present is their inability to precisely and symbolically reason. But if they’re able to do any symbolic reasoning at all, then inductively, they should be able to do more symbolic reasoning. This suggests to me that the transformer-LLM architecture may actually scale to true (and correct) symbolic reasoning, which I regard as pretty much the Holy Grail of this branch of machine learning.
A Dumb Turing Machine
We observed that LLMs appear to have some limited capability for symbolic reasoning, particularly for adding two numbers. We saw performance degrade as we tried to add more numbers, but there’s a workaround.
I mentioned at the start that you may argue that GPT can reason if you give it some memory and many iterations over which its language inference turns into (fuzzy) symbolic inference. GPT will correctly compute long addition sequences, just like the ones we saw earlier, if you prompt it to proceed two numbers at a time.
It worked. You can check out the live example here, in which I had GPT compute the sum of a length-24 sequence — something we couldn’t do at all in the naive prompt.
This “scratchpad” technique is a popular technique in working with LLMs: you have the LLM write down intermediate results and then explicitly use those results to continue working. You can chain arbitrary scratchpad steps together, though it may require re-prompting.
Abstractly, the idea of keeping and adjusting a memory register for every computational step reminds me of a Turing Machine. You can imagine prompting the LLM as I did, using its language capabilities to break a symbolic reasoning task into tiny steps that it can handle symbolically, and using a memory register to store the intermediate values so it doesn’t get overwhelmed. Basically, you can prompt to implement a Frankenstein Turing Machine inside an LLM. This is sort of neat — a way to purely use LLMs to solve symbolic reasoning tasks, which is what we’re all after. But it’s also sort of dumb, because your computer is already a Turing Machine, simulating an LLM, in turn simulating a Turing Machine. My intuition is that the way to get LLMs to reason symbolically at scale is probably not by brute-forcing it via Dumb-Turing-Machine-style computation, but maybe it is. Intuitition for LLMs is tricky — I’ve been wrong several times just in the course of writing this blog post.
Appendix Bonus Material! Prime Factorization
This was another experiment I conducted that didn’t really fit well into the discussion piece above, but I thought might be of interest to some of you.
The theme of “close approximation” raised a question: when GPT-4 was incorrect, was this straight-forward hallucination, or something more subtle, like a token being dropped or double-counted? In my work with LLMs at Limit, this is something I’ve seen frequently: LLMs are biased toward interpreting the beginnings and ends of prompts, and the longer your prompt, the greater the probability that instructions from the middle are not followed.
There’s an arithmetic way to test this. It relies on the fact that every integer greater than 1 is the product of a unique set of prime numbers. For example, the prime factorization of 38 is 2 and 19, and the prime factorization of 8 is 2, 2, and 2.
Therefore, I could ask GPT to multiply a set of prime numbers, and then I could compute the prime factors of the number it returned, and check the difference. By way of example, suppose:
My prompt is “multiply 2, 3, 5, 7, 7”
GPT returns 2646
The unique prime factorization of 2646 is 2, 3, 7, 7, 9
Therefore, while GPT multiplied the digits 2, 3, 7, 7, it omitted the 5 from the prompt and included a 9.
However, the results were nothing like this. Even for a sequence of only 5 digits, any overlap in prime factors seemed no more significant than chance. An example result below:
Prompt: 37, 37, 47, 47, 127
True value: 384,063,367
GPT result: 1,213,787,489
GPT result prime factorization: 29, 41854741
Or:
Prompt: 11, 13, 19, 43, 47
True value: 5,491,057
GPT result: 203,679,161
GPT result prime factorization: 7, 4973, 5851
I’ll spare you the many other examples. Unlike the results in addition, when it comes to multiplication, the results are wildly off. There were no close approximations to be seen in the results, and I couldn’t find any relationship between the prime factors I was using as input and the ones I was getting as output. After looking into it more, I found a paper extending this topic, Positional Description Matters for Transformers Arithmetic, which you may find interesting.
For clarification, what I mean by “symbolic reasoning” or “symbolic inference” is reasoning according to strict rules that are represented by symbols. The most classic example of symbolic reasoning is in solving mathematical equations.
To me, this is a contrast to inference in language, which is very fuzzy: if I start a sentence with “I am going to the store today,” then there are many ways to complete the sentence that would be acceptable, and an LLM will do a great job at generating them. However, if you have a sentence like “94 + 281 * 289 =” then there is only one precise way to complete it (in simplified form).
The notion that GPT can use its language inference capabilities to do symbolic reasoning is something I address toward the end of the piece, in the section “A Dumb Turing Machine”.
For example, “2 + 6 + 9 + 87 + 57” is a sequence of length 5.
If you wanted to test this formally, you could follow the approach of certain academic papers, run your own LLM, and then observe which neurons are activated when processing a given token.
Another potential implication is that the sum-syntax might work better because it’s just fewer tokens/symbols overall?
For example, translating from Polish to French, or converting CSV to JSON.
I say “the results of actual addition” because it is not clear that it is approximating addition as in the symbolic reasoning process. (By way of hyperbolic example, a lucky guess does not approximate the execution of a specific process; at best, it may approximate the results.)